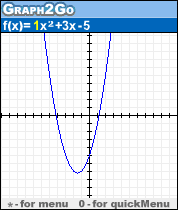
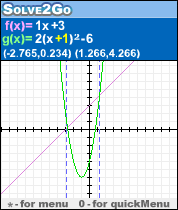
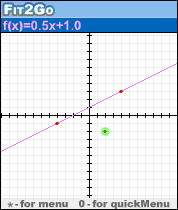
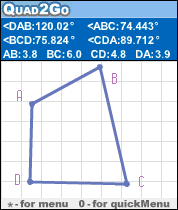
Graph2Go
圖形計算器在教學和學習數學中非常有用。它�?�一個支持概念性理解一般的功能,特別�?�學校代數和真實分析的環境。特別地,它增強了圖形和符號表示之間的連接。代數教學的一個主要目標�?�為學習者提供工具來數學化他們的感知。多重表徵方法有可能將解決甚至傳統問題的重點從分配和解決未知的問題轉移到分析各個過程和這些過程之間的關係。多個功能表示的集成為開發更廣泛的傳統問題的解決方法創造了機會。放大使用圖形計算器,研究人員指出四種模式和使用模式:計算工具,數據分析工具,可視化工具和檢查工具。 動態變換�?�Graph2Go的獨特功能。動態控制涉及對對像或數學對象的表示的直接操縱。由於驅動輸入�?�字母符號,所以對函數表達式中涉及的數字執行轉換。因此,通過參數化一個例子,我們把它變成一個函數族。研究表�?�,用戶和屏幕上的對...
閱讀更多